The Quest For Absolute Nothingness

[Jonathan Barlow Gee]

"The Quest for Absolution In Nothingness" :

An Exploration of Nothingness for the Pythagorean Order of Death.

by: Jonathan Barlow Gee, Tallahassee, Florida, America; November 6th, 2014.

Abstract:

According to the majority of both scholarly and speculative QBLHists following the 1st century AD, beyond the boundaries of our universe there were three layers, comprised of light (called "ayin soph aur"), a form of glowing gloom or gloaming alike twilight (called "ayin soph") and an utterly unlimited abyss of empty darkness (called "ayin"). In this essay, the nature of these three levels and layers is explored and their meaning applied to the schools of modern astro- and particle-physics as well as to traditionally "Pythagorean" schools of number-theory. The number-sums "∞" ("infinity"), "ø" (the "empty set," meaning "absolute zero") and "1" are explored as they relate to the "Pythagorean triangle" method of "Gnomonic" expansion rate, and ultimately equated to the "nulliverse" of "ZPE," the "multiverse" of "baby universes" inside of black-holes' core-most gravitational-singularities, and to the smallest scale of quanta as "matter" with "mass," respectively.

contents:

Part 1. The Value of Meaning In Absolute Nothingness

Part 2. The Quest for Absolute Nothingness in Mathematics

Part 3. A Brief History of Absolute Nothingness (and What Lies Beyond)

Part 1. The Value of Meaning In Absolute Nothingness

If we venture into the realm wherein physics is defined as being (at least partially) "imaginary," and the "universe is mental" becomes an at least partially applicable law allowing "mind over matter," etc., then we may say, firstly, that "some things we see are not real," but this should immediately be followed secondarily by the statement of rules that must then be put into place to define what determines what we "see" that "is real" vs. what we "see" that is "not real."

For example, I can look at a tree and say, this thing is "real," it has mass, matter, substance, density, chemistry over relatively long durations of time compared to my own, etc. I can even look at a desk that has been made from lumber milled from the felling of that same tree and say, about the desk, "yes, also, this is real. It has the same mass, matter, substance, density, chemistry over relatively long durations of time compared to my own, etc. as the tree, even though now it is in the form of this desk or these cabinets or this chair or this set of 900 toothpicks, etc."

But if it is the "mass, matter, substance, density, chemistry over relatively long durations of time compared to my own, etc." that gives this "tree" or that "desk" or this "pencil" objective reality, there is just as valid an argument to be made that the majority of the area we perceive being comprised by the "mass, matter, substance, density, chemistry, duration, etc." of the "solid material object" is actually comprised of empty space and void, and that only on the smallest possible scale do the smallest possible amounts of mass, matter, substance, etc. even exist at all; all the rest is merely an optical illusion of our perception, filling in the blank gaps with color-coded wavelengths of energy. So if you say, "this tree is green," or "this pencil is yellow" it is not the actual "tree" or "pencil" you are describing, but the colorful illusion they cast between their very minuscule portions of "matter" with "mass."

According to Aristotle, whom was an exceptionally untalented record-keeper, the Pythagoreans, following their venerated elder Pythagoras of Samos and of Croton, believed that, due to their cherished axiom "all is number," it was thus also possible to assign to any given living being a certain number as well, and this was described (again falsely attributed by Aristotle to the Pythagoreans) as being possible to depict using a chalk-outline of the person's body and a certain sum or other of a certain sort of bean. This was never believed to be a literal rather than allegoric mental exercise by anyone besides Aristotle, but nevertheless the legend stands, and little is known beyond it of its originally intended meaning. If one considers "beans" as being merely a metaphor for "atoms" (the theoretical, smallest constituent component particle believed to exist at that time, as posited by Democritus), then in truth each person and each living being is made up of a different certain sum of these, but this certain sum may be constantly changing over time.

So it would seem there is a great deal we actually, literally SEE with our "naked eyes" that is actually a smudging together, like in pointillist painting technique, wherein multiple variable factors are combined into one averaged "lump sum" and these portioned off by segments along a pre-arranged, although entirely arbitrary and imaginary, format for order.

But I also stubbornly KNOW with the substance of my OWN being that there are some objects that are "more real" than others that are "less real." For example, when I blow smoke through the netted screen wall of my porch, it passes through virtually unimpeded; but if I blow smoke against a glass window pane on the front of the house, then the smoke disperses and cannot penetrate the glass to permeate within to the inside of the house. This is simple physics; over-simplified: the "glass" is verifiably tested and proved to be "more real" than the "screen." Thus, the "degree" of "realness" may be determinable according to a factor of information membrane-permeability; a way of opening all circuits in a series simultaneously to their fullest capacity and allowing information and electrical coding to flow through at their least impeded pace of rapidity. Conclusion: "hard ice (encryption software) is MORE REAL than soft ice."

What is "least real" of all in this mental-map superimposed invisibly overtop of "reality" (comprised ONLY of what is matter with mass) is the "mind" itself imposing this "memory-castle" overtop of, upon and onto, clinging to, the "atomic" matter format. This is because the "mind" (because it can conceive of and perceive of all this, "understanding" it all by objectively positioning itself ABOVE it all) is thus capable of containing ALL the other levels and layers of such a reality, and is thus, itself, comprised necessarily ONLY of the SMALLEST POSSIBLE format for such levels and layers of such a reality to occur - in this case the ZPE of "quantum foam" or superluminal tachyons.

And so we see a sea of quantum-foam, a "nulliverse" of ZPE, a "primary clear light" of transparent superluminal tachyons, such as so-called "Cerenkov radiation," stretches out even beyond the "multiverse" of smaller, bubbling-off branching off-shoots from the main-stream "time-line" of the "local universe" in the form of "baby universes" born inside the singularities at the cores of black-holes, themselves at the cores of spiral galaxies, these spiral galaxies all arranged along a single long filament, a "loop quantum gravity" super-symmetrical "string" of sub-quantum, superluminal Calabi-Yau shaped "extra-dimensions" (in potential, alike the 3 of space, but which never "expanded" following the "big bang").

Part 2. The Quest for Absolute Nothingness in Mathematics

Given a pythagorean right-triangle, where the sum of the squares of legs a & b is equal to the square of hypotenuse c, expressed: a^2 + b^2 = c^2...

Let the square of the length of one leg of the triangle be equal to the single unit-cell square area of "1^2" and the square of the length of the second leg of the triangle be equal to the area of 2^2 or 4 times the area of the initial unit-cell square. The length of the hypotenuse is, then, given as the sum "3," such that the lengths of the three measures of length around the Pythagorean triangle are "1,2,3."

Now, under these given conditions, let us "explore the space." If the "square of 1" is "1^2," and the "square of 2" ("2^2") then the "square of 3" is "3^3," such that, if under the conditions of "a^2 + b^2 = c^2" then "1^2 + 2^2 = 3^2." This, prima fascia, is acceptable, unless we begin to examine it in more detail.

If "1^2 + 2^2 CAN = 3^2" then the "square" sum of 1 MUST be (or be ABLE to be, under specific conditions) equal to the sum of "5." This is because, under these conditions ("a^2 + b^2 = c^2"), where "1^2 + 2^2" MUST "= 3^2," given that (under ANY conditions) 2^2 = 4 and 3^2 = 9, and 9 - 4 = 5, thus the only remaining sum in the expression to compute to the sum of "5" is "1^2," then, under these conditions, it must be possible for the "square of 1" (or "1^2") to be "= 5."

So, let us explore how and why it is, under these given conditions, that the value of the sum "1^2" (or "1 times 1") and the integer "5" can be the same. In the ancient Chinese study on gnomons, the "Zhou Bi Suan Jing," where the original "Pythagorean triangle" was first noted generations prior to Pythagoras' own lifetime, the same example as, later, attributed to Pythagoras by Euclid is given for it as a "3,4,5" triangle, where the sums of the squares of the legs neatly sum the square of the hypotenuse ("3^2 = 4^2 = 5^2"). However, in this example in the "Zhuo Bi Suan Jing," the interior of the "5^2" aspect is also delved into in more depth.

The "5^2" area is depicted as surrounding a "3^2" area, as, it is implied, is the "3^2" area then meant to graphically depict the same relationship of area surrounding (as a circumferential, square expansion) the single unit-cell square used to begin with. Thus, the "3^2" is a "Gnomonic" expansion of the "1^2" or single unit-cell area square, in the same way as the "5^2" is to the "3^2." In this manner, we can see a relationship beginning to form between the concepts of the "single unit-cell area square" of "1^2" and the concept of the "5^2" or the "integer 5" in itself.

There can be two different sorts of this type of "Gnomonic" expansion rate. One begins with the "unit-cell area square" or "1^2," continues to "3^2," thus to "5^2," thus to "7^2" and thus to "9^2," etc. ascending through all the "square sums" that have odd integers as their #-base (rows times columns = order). The other type of "Gnomonic" expansion rate thus encompasses the "even" integer's "square sums" or "exponential" set (thus "2^2, 4^2, 6^2, 8^2, etc."). Pythagoras, according to Iamblichus, labeled these sets "clockwise" and "counter-clockwise" or "right" and "left" ("handed") and thus related all "even" numbers with "outward expansion" along a "clockwise" spiral and all "inward contraction" along a "counter-clockwise" spiral he related with "odd" numbers.

What Pythagoras sought was a sequence that "expanded from" or "contracted to" the smallest possible scale set of numbers; what would have been, for math, the equivalent of what the contemporary "atom" of Democritus was for physics. Theodorus of Cyrene, a 5th century mathematician, is credited with creating what Pythagoras would have called a "right handed, expanded" spiral based on what Euclid would have called "Pythagorean triangles," and it has been noted that this spiral includes measurements that can be rendered as "square roots" (the row or column per any integer taken as a "square" order, reverse engineering the length of the legs given the length of the hypotenuse), even "square roots" smaller than the smallest then known integer "1."

Because Pythagoras disliked what he called "incommensurate multitudes" (imbalanced equations resulting from factoring fractional or decimal-place integers occurring BETWEEN whole numbers) his followers, according to legend, threw "Ceylon" (who brought his knowledge about "square roots" smaller than "1" to the attention of Pythagoras) overboard from a boat. However this knowledge was obviously not lost, nor wasted in this manner by applying it as such to the "spiral of Theodorus."

So, if "1" and the "square root of 1" are both measurable as the same length, it was reasoned early on, then the length of the hypotenuse drawn to connect these lengths, if they were arranged at a right-angle to one another, would be equal to the "square root of 2." This disagreed with Pythagorean number theory, which began the series of "counting numbers" with the non-integer "zero," because "zero squared = zero" in the same way that "one squared = one." Thus, the early Pythagoreans apparently believed that there was such a thing as the "square of zero" or "0^2" just as the "square of 1" would be "1^2" (where the legs were rows and columns, and the hypotenuse a diagonal between them expressed as a multiple of the rows times the columns).

So, according to Pythagorean number theory, if there were a "square root of one" it would arise as the diagonal hypotenuse between the equal legs of length "1". If the triangle of lengths "1, 1, √1" is both a Pythagorean AND an equilateral triangle, THEN it would be proven that the "square root of one" had the same length, or was a measure of the same distance of area, as the length measured by the integer sum "1."

However, to the Pythagorean number-theory system of thinking, the third side of such a triangle would not be labeled by the abstract principle, or specifically "incommensurate multiple," called the "square root of 1." Instead, it would correspond to "zero" because, in Pythagorean number-theory, "zero" was counted as a whole number.

Thus, in Pythagorean number-theory, "zero times zero would = one;" "one times one would equal two," "two times two would equal four" and "three times three would equal nine." Because "two" is "even" and "three" is the first "odd" number counted by Pythagoreans, the spirals of subsequent exponential expansion formed from squaring two and squaring three are depicted in the shape of the Arabic numerals themselves as "6" and "9," one clockwise, one counterclockwise.

If "one" is the sum of "zero squared" or the multiplicative product of "zero times zero," it means that "zero" has implicit length as an area in and of itself that CAN be measured as distance over space; at least in Pythagorean reckoning. Zero would thus NOT be the "smallest number" in the model of Pythagorean number-theory seeking to find the "smallest indivisible sum." So what is this individual "smallest indivisible sum"? To Pythagoreans, it would have been a sum that cannot be any further sub-divided, and so this smallest sum would had to have stopped counting down at "zero," because "zero" is "indivisible" (by anything besides itself alone, not even, like all other prime numbers, only by itself and one). However, if "zero" also has a measurable area, and covers a distance of some amount of space that has substance, that can be summed up, even as empty void, then it also cannot be considered to be the smallest "indivisible" sum.

If "zero" is not the "smallest indivisible sum" then what is? The answer is clearly obvious, to one with "eyes to see." However, to those without let us lead up to it a bit, for the sake of entertaining ourselves at the expense of their amusement being turned by us into amazement. If "zero" is a "void" what is it filled by? Or, more accurately, if "outer space is empty, what smallest form of micro-energy fills this vacuum?" The ancients called the modern "Akasha" or "Chi" the "Vril" or "Thule," but the idea was the same the students of physics know of as the "Ether." Modern physicists speculate about a "ZPE" field of "quantum foam" above the "speed of light" comprised of "tachyons," but the idea remains the same. So, what number sum can one use to express this concept as being also "smaller than zero"? Simple: "∞" or "infinity" itself.

Thus, the smallest possible "Pythagorean triangle" that could be formed, according to the reckoning of ancient Pythagorean number-theory, was not, as given by Euclid and in the Zhou-Bi-Suan-Jing as the "3,4,5" triangle, nor even the smaller, more speculative "1,2,3" triangle, but would have been the ultimate, atomic, sub-atomic and quantum spectrum level measurement scale: a triangle of "∞, ø, & 1".

So, if we begin by looking at the smallest level of physics in terms of the smallest sums in Pythagorean number-theory, we can equate the "ether" or "ZPE" to "∞," the empty void of outer space beneath light-speed to "ø" (or "the empty-set," meaning the "absolute value of zero" as opposed to the "relative value," an idea we will discuss in a moment), and the smallest particulate matter or "quanta" we can then equate to "one," the THIRD "whole number" in the "counting series" of Pythagorean number-theory. If "∞" were a cup, and "1" were a liquid poured into it, then "ø" would be the empty void, and when filled up, as whatever amount is left unfilled.

So how does "zero" originate out of "infninity," and how does "one" emanate forth from "zero"? If the moment of the "big bang" caused our universal singularity to begin expanding, and before this "nothingness" existed rather than any kind of "matter," then we could likewise count the moment of the "big bang" as the "first instant" of time, and thus on a time-line number this event as the integer "one." But then, what preceded this event, and caused it to occur?

Let us begin by looking at how the outline of a torus is formed due to precession over time of the polar axis of an orbiting spherical volume in space. We can see how a volume in space is initially condensed into a sphere, in the blue "pi" spiral spaces, and how this sphere, by orbiting centripetally in an ellipse around a centroid location will, over time, result in the distortion from perfect perpendicularity of its orbital plane known as "precession," labeled as the red "phi" spiral. The purple horizontal line signifies the axis of rotation of this orbiting spherical volume's centroid location as being, in turn, relative to the next nearest strong gravitational influence as well, and thus this model of the torus serves as, itself, a "unit-cell" within a larger system, accumulating based on similar "unit-cell" shaped bits of information.

But how do we measure these motions in a vortex space in such a way as to model them as "unit cells" that can be accumulated to form a larger system of similar shaped bits of information? If we were wanted to take the above model of a torus shape, and slice it exactly in half across its averaged horizontal circumference, the "equator" of the figurative "hyper-sphere," as we would slice a breaded bagel in half to spread cream-cheese on it by creating the largest interior surface area possible, we would be do so by using and creating a "lorenz transform" of all the combined motions occurring in this toroid model's manifold surfaces.

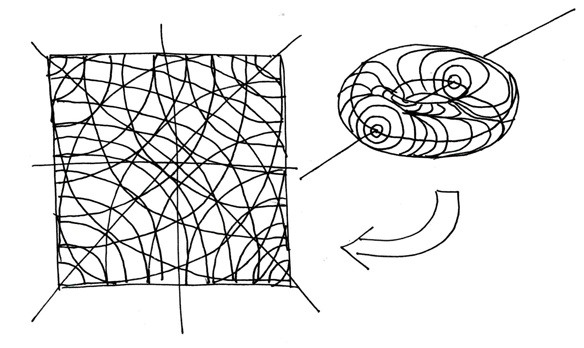
In this diagram we see such a "lorenz transform" of the above toroidal model's equatorial motions. The axial line shown piercing through equant points on the torus in the upper-right of the diagram is equivalent to the diaganol line bisecting the "lorenz transform" square-well on the left from the upper-right corner. In the model of a "lorenz transform," the "field-lines" shown as expanding and contracting circumferences of latitude on the topology of the torus become the semi-circles emanating out from each of the 4 corners of the square, while the 4 corners themselves become the 4, equidistant points on the torus where the axial line pierces the torus. Thus the axial line piercing the torus is not only the 1 diagonal line crossing from the upper-right to the lower-left, but BOTH diagonal lines, including the one crossing from the lower-right to the upper-left. This is because the axial line is shown as "within the boundary of the square" (lorenz transform) ONLY where it is measuring the surface area of the torus itself, that is, where the axial line is IN CONTACT with the surface area of the torus: thus, the axial line proceeds on the lorenz transform from the upper-right corner to the center, then changes direction and proceeds to the upper-left corner; this is because it is reaching and then passing the "centrality" point inside the "pi" spiral interior of the torus along this path. The "mid-point" of the "lorenz transform" and the origin-point of the "pi" spiral bisection of the "tubular" circumference of a "torus" are the same. The axial line then "breaks the space" to cross the torus' empty central "hole," and then returns on the "lorenz transform" to perform the same motion, entering from the lower-right corner and exiting again at the lower-left.

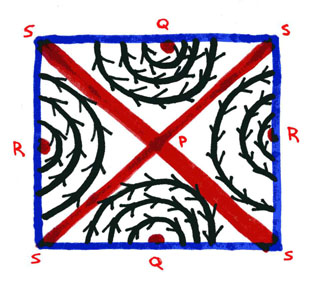
Now, this "lorenz transform" image, capturing the directions of motion possible on the surface of a torus, is interesting for another reason than beside merely its harmonic resonance and usefulness in the field of particle physics. It appears, in the realm of mathematically-based theoretical physics, in the same form as shown as a "metric tensor" or mathematical construct with accompanying geometrical diagram. In Stephen Hawking and Roger Penrose' work "Geometry of Space and Time," they mention the "static metric" of Dutch mathematician and astronomer Willem DeSitter. This model, which we shall be examining in more detail next, shows us the same essential pattern as a "lorenz transform" for a torus, but it is describing the laws constraining physics near the surface of a black-hole. In both the "lorenz transform" of a torus and the "DeSitter metric tensor" models, what we are seeing is how the infinite, perpetual motion of a torus may be mapped and thus contained into the measurement, valueless in and of itself (unless used as a unit-cell inside a larger, similarly structured system), which Pythagoreans measured as "zero squared."

Again, however, let us pause to consider that the "ZPE" of "tachyons" in "hyperspace" may be "infinite," and the limit of outer-space's vacuum being defined as all that exists below the speed of light may be a frictionlessly permeable membrane (measuring "zero" resistance) in itself, yet if we depict these graphically as a torus and a "lorenz transform" (sqaure) thereof respectively, they may combine to produce "something from nothing" by creating a basic "unit-cell" that can be replicated across multiple levels of size-scale to accure into a larger information processing system. In short, we are studying the application of "Pythagorean number theory" concepts of very small number-sums as labels to geometric graphs of models based on hyperspace rules for topology and motion, and doing so to understand the nature and physical properties of the smallest size-scales of our cosmos and thus expand our knowledge of our material reality.

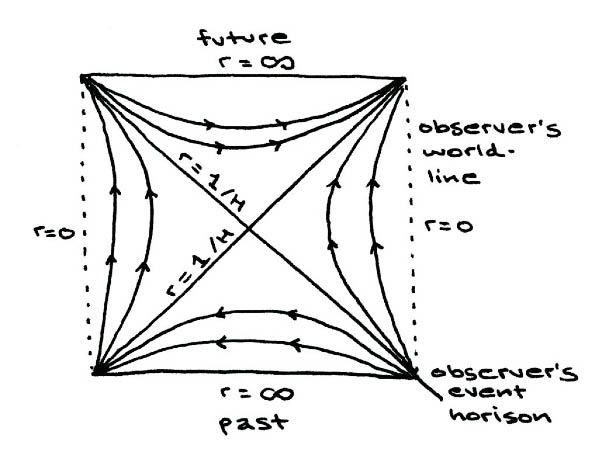
In the "static DeSitter metric," what we are seeing is a description of a form of physical event predicted as possible according to Einstein's "relativisitic" laws describing cosmic scales of gravitational force. When a large amount of gravitational pull is being exerted from a body of mass in the relative vacuum of space, one would expect its volume to be commensurate to its influence and pull, but Einstein predicted this did not have to always be the case. In certain circumstances, what Einstein predicted as "gravitational singularities" (later called "black-holes" due to their ability to swallow up even energy moving at the speed of light) could have a very strong amount of gravitational pull on neighboring heavenly bodies, but still be of a microscopically small scale of size in terms of volume. These, Einstein predicted, had large gravitational pull due to having large amounts of mass, but they kept their mass not in the form of "volume," but in the form of "density." Thus, an ultra-dense "black-hole" could hold the same amount of mass as a much larger heavenly body (even more than a star), and thus exert the same amount of gravitational pull. Later on, it was found that "gravitational singularities" have formed "black holes" in our cosmos and that it is these same gravitational bodies that have attracted around their equatorial accretion discs the spiral galaxies, each comprised of billions and billions of stars, seen beyond our own "Milky Way" galaxy in the Hubble satellite deep field images and those captured from other, earth-bound observatories. In short, if you wanted to graph what the exterior surface of a "black hole" would look like, in terms of its gravity-well's bending to the surrounding fabric of the spacetime continuuum (in the form of the "microwave background radiation" of surrounding photo-electricity), the result would depict the central spiralling vortex of a torus, with a rotating polar axis of "ejecta" (the tachyon-speed iron-gas jet-clouds streaming from the "white-holes" at the magnetic poles of gravitational singularities); so it should not be surprising to find the "lorenz transform" of a torus show up in the "DeSitter metric tensor" as a geometric graph of a black-hole.

In the "static DeSitter" what we find depicted is a pair of perpendicular diagonal lines, both labeled "r = 1/ H" (where it is explained in context that "H" = "Hubble's constant" and that, thus, "1/H" would be the "reciprocal" of "Hubble's constant;" and where "r" is short for "radius"), a pair of parallel vertical lines, both labeled "r = ø" (expressing the fundamentally integral concept of "ø" as symbolic of a "singularity" - that in the densest core of a gravitational singularity, or "black hole," time stops), and a pair of parallel horizontal lines, perpendicular to the parallel lines (both labeled "r = ø") that are, in turn, each labeled uniquely (the lower is labeled "r=∞ past" while the upper is labeled "r=∞ future"). The lower right corner is labeled "observer's event horizon," meaning their location in space-time at the edge of a black-hole, and the motion (indiciated by curving arced arrows) of spacetime in front of the "observer" is labeled as the "observer's world-line." Notice these arrows proceed to emanate away from the lower-right corner and toward the upper-right corner.

It is possible to use the "static DeSitter metric" as a base unit-cell inside a "gnomonically" expanding system of similar information-bits, parsed across a variegated size-scale. In short, it is possible to use the same geometric model based on the "lorenz transform" of a torus to symbolize "zero" as a "place-holder." Graphically, doing so creates a basic "cell-unit" that repeats over a "Gnomonically" expanding cyclical pattern, resulting in a curving around this central-point along a diagonal axis over time of the ether (ZPE) in a pendulous (swinging "back-and-forth" motion), "stirring" it such that, during the first "Planck-time" following the "big bang," the 4 elemental forces of our present cosmos were divided and differentiated as various different wavelengths and frequencies of force by this process.

In this model we see the manner in which this "stirring" motion within the ZPE during the first Planck-time immediately following the "big bang" event that began our cosmos divided and differentiated the 4 elemental forces of the cosmos. The size-scale of the lorenz-transform / DeSitter metric shown in red in the lower right corner is slightly larger than the same depiction of a lorenz-transform / DeSitter metric shown in black in the upper-left of the right 1/2 of this diagram because the wavelengths defining the force of fusion (that governing quanta on the scale of quarks and leptons) are slightly larger (and their frequency slightly longer) than those expressing the force of gravity (that defining the smallest scale of quanta, defined as a "gravitational singularity" and shown only as the transform / metric in black). Within this model are shown smaller isomoprhic loop-based shapes and forms, each color-coded to the 4 elemental forces as well, and these represent the organizing influence the preceding, smaller size-scale force has on the next larger size-scale force. For example, the black "transform / metric" of gravity effects the "electromagnetic force" (in blue) to generate, at that size-scale, the form of the torus depicted in black; the blue "transform / metric" of electromagnetism effects the force of "fission" (in green) to generate, at that size-scale, the form of the isomorphic-loop depicted in blue; etc. At the lower right corner of the entire diagram, there is a small, simplified depiction of the "transform / metric" unit-cell labeled with "N" in the center (meaning "NAM," cognate with "fate," "free-will," the present moment and with self-determination) and with 4 "NT"s around it (meaning "NAM.TAR," cognate with "destiny," "predeterminism," the past and future, and with theology). This origin-point labelled "NAM" in this "key" occurs for each of the elementally color-coded base unit-cells of transforms / metrics at its mid-point at a location labeled in the diagram on the left by the arcs with distances determined by a "gnomonic" expansion rate. Thus, the transform / metric base unit-cell's centroid-point is shown at the size-scale for the force of "fusion" (in red) as the arc on the left labeled (likewise all color-coded to represent "fusion" in red) "r = 1," while the transform / metric base unit-cell's centroid point is shown at the size-scale for the force of "gravity" (in black) as the arc on the left, which would be labeled as "r = √16". In this model, the significance of "1 = √1^2" is also shown as being the difference between the "relative" value of "1" (as in situations wherein "1" is used as a coordinate, or is used otherwise "relative" to other variables or integers) and the "absolute" value of "1" (as in situations wherein "1" exists in isolation and in absentia of ANY other variables or integers as an "absolute" value in and of itself).

As mentioned previously, there are also an "absolute" and a "relative" value of "zero." It is thus also that "zero" has a different form of value when it is in "relationship" to or "correspondent" with other variables or integers than it has when it is not and when it is, rather, isolated as an objective thing in-itself or when it is not. "Zero" is thus a "relative variable," and not necessarily an "absolute" in itself as it has been upheld by most mathematicians of western science until the modern time. Only in the tandem, parallel Pythagorean school of number-theory did the tradition survive preserving "zero" as a "relative variable" rather than as an "absolute value." However, in truth, "zero" is neither only a "relative variable" NOR an "absolute value," but both; and so we see that there is a form of "zero" that expresses the vacuum of the cosmos defined as outer space below the limit of light-speed, and there is a form of "zero" that expresses the void of resistance against "zero-point energy" or tachyons, providing them with their ability to travel "faster than time" by yielding "zero resistance" to their unimpeded asymptotic liberation into entropy. Thus, there is a form of "absolute zero" (symbolic of the vastness of the vacuum of outer space) and a form of "relative zero" (symbolic of the very small void between quanta in "hilbert space") even in modern astro- and particle-physics.

Part 3. A Brief History of Absolute Nothingness (and What Lies Beyond)

Did you know that some people do not even exist? Did you know that some people are not even there, that they only look like they are there, but that this is only an illusion, a hallucination induced from outside onto your own mind, and that there is, in fact, either no one there in reality or, worse, someone or something else, using that image as a camouflage for something even more sinister?

And when we have a NDE, such as in an automobile accident, especially if under the influence of a sensory intoxicant like alcohol, or if we practice the experience of attaining NDEs by use of drug over-dose such as many modern "urban-shamans" do (MANY folks I know online do this), eventually we will hit this "brick wall" of the "primary clear light" or the "nulliverse" of ZPE, the vast ocean of pure tachyons awaiting just beyond the speed of photons in a perfect vacuum. This experience of attaining such a perspective as from the "most high" looking downward upon the entirety of the cosmos before them is, shall we say, an "acquired taste." It may be unique to our species, and this dates the perception of this phenomenon only as far back as some 6000 years ago (when we developed the agrarian revolution following the Mesopotamian flood that had wiped out whatever we may have had going on prior to then). Nevertheless, in these 6000 or so years the "primary clear light" has been called "ylem" by Buddhists, "heaven" by western monotheists, and is believed, by the 3 major world religions today, to be the abode of an abominable imaginary man who lives in the sky behind the clouds and who hates us and wishes we'd get off his lawn.

For example in the Apocryphal "Book(s) of Enoch" it is quite clear, as our other earliest historical records corroborate as well, that the use of hallucinogens to "make contact" with the monotheist deity itself was common even long prior to the Mesopotamian deluge.

Enoch was a shaman. He ate the shem-manna, the "bread from heaven" which was the "food of the gods;" this means he partook of the natural hallucinogenics that were available in the ecological pharmacopeia of his day. The "visions of Enoch" describe quite clearly certain details that can only have been visualized from a perspective far removed above the surface of the earth, perceived (though round) as though a flat plane. However, there are 3 "basic" explanations bouncing around today as to how and why this could have occurred: 1. "God" is real. This is highly unlikely, so much so, I would not venture to debate its validity. 2. "Aliens abducted Enoch." This is also unlikely, although no less possible (from his personal mental perspective) an explanation for his experiences than the monotheist deity. 3. "Enoch was Stoned Ape patient zero." This explanation I find most satisfactory, because it carries over the theme of shamanic drug-use from pre-deluvial to antediluvian eras. The basis of "king" on the tribal elder's role as "chief" and of "priest" on the tribal shaman's role as "medicine man" is fundamental to most modern anthropological theories of civilization's origin.

However, AGAIN, what else is this "monotheist deity" BUT the "mind"? Because it can supersede all these "layers and levels" of reality, and is thus comprised of the smallest, fastest, least massive particulate energy format, accumulating the least resistance possible, accruing the least amount of friction possible, etc. the "mind" out-races, out-paces, and out-reaches all forms of matter-energy, and then stops, turns around and confronts us in the form of "god," our own "mind" alienated from us.

So the mind can travel faster than photons in a pure vacuum more easily than it can part with its own self-concept, and so it narcissistically clings to its own reflection in the form of a projected, imaginary "god." Think about this. Since the era of Babylon in the majority of the "civilized" world, it has been the law of the land that some form of "theism" is true. What if it wasn't? What if there IS NO SUCH THING as "God"? Due to 6000 years of conditioning, the mind can more easily fathom the facts proposed by radical atheism than it can accept the full spectrum scope and scale of actual, radical atheism to its entire concept of reality. If there is "no god," this does not mean there is "no heaven," nor, rather, no "primary clear light," properly called "hyperspace." Hyperspace is real, the cosmos is the "heavens," and in the afterlife, the soul may explore these, according to the predictions of mankind's historical shamans.

But hyperspace is "less real" (more permeable) than "solid material reality" (less permeable), and the mind beyond these both less real still; and so we see that, from the point of view of material scientists, "hyperspace" is merely a theory, while even to "hyperspatial" meta-physicists like myself the existence of the "universal mind" as being a "true" monotheist deity remains conjectural, abstract and absurd.